現在位置のナビ
トップ → コンピュータの国 → 雑記帳 → 趣味趣味音響 → スピーカーに伝わる駆動力
説明
スピーカーに駆動力が加わったときの、振動板の挙動を考えます。
なぜ電流帰還アンプにこだわるのかに書いた章立て案の§2.1に含まれる内容です。
モデル
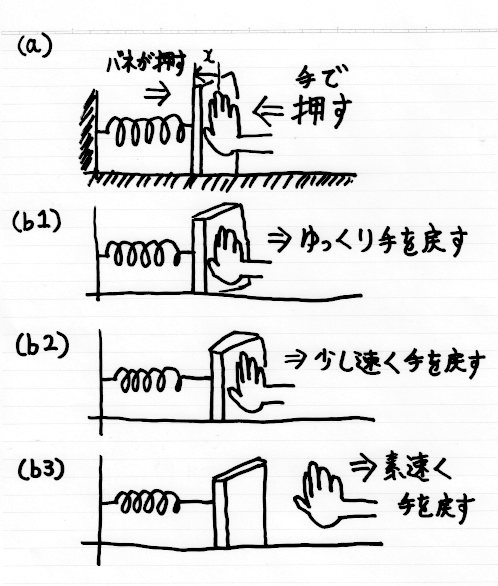 図1 スピーカー振動板へ伝わる駆動力のモデル
図1 スピーカー振動板へ伝わる駆動力のモデル
スピーカー振動板へ伝わる駆動力を、図1に示してみました。
図1(a)は、力学的に均衡している状況です。
振動板を押す電磁石の力と、押し返すバネ(サスペンション)の力が等しくなり、振動板は静止しています。
図1(b1)は、力学的に均衡している状況を保ちながら、振動板が移動している状況です。
図1(b2)は、振動板を押していた手が速く戻っています。
手はすでに振動板を押していないのですが、バネが押し返す速度と、手の戻る速度が一致しています。
図1(b3)は、振動板を押していた手が素早く戻っています。
振動板を押し戻すバネの力が足りず、手と振動板が離れてしまっています。
図1の(b1) (b2) (B3)は、駆動信号の周波数によって、駆動の仕方が違うことを示しています。
スピーカーユニットの固有振動周波数をf 0とすると、(b1)はf 0以下の低域、(b2)はちょうどf 0 、(b3)はf 0よりも高域を示しています。
ブランコの例え話
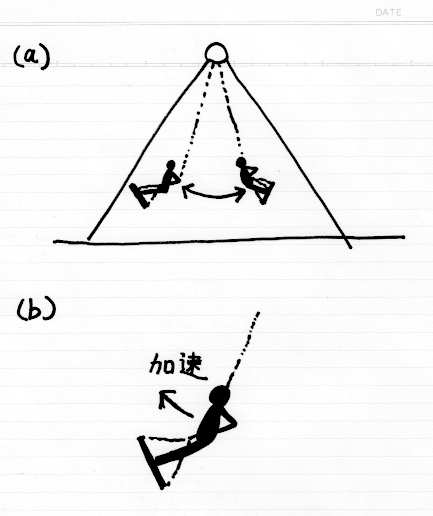 図2 ブランコの駆動力
図2 ブランコの駆動力
ブランコの駆動力を図2に示します。
ブランコを漕ぐ時、外から力は加えません。
乗っている人の重心移動だけで運動します。
図2(a)では、ブランコを前に漕ぐ時に、重心よりも前に板を押し出す様子と、後に漕ぐときは板を後に押し出す様子を示しています。
漕ぎ始めでは、重心移動が一番大きくなった時、ブランコの揺れも大きくなります。
図2(b)では、重心移動でブランコを加速している様子を示しています。
漕ぎ始めてから時間が経つと、重心移動で揺れが最大になるのではなく、揺れを加速するために重心移動を用います。
漕ぎ始めで「重心移動の最大=揺れの最大」となるのは過渡応答であり、「重心移動の最大=加速の最大」となるのは定常状態です。
これと同じことが、スピーカーの駆動でも起きています。
周波数帯別スピーカーの駆動
モデルと例え話から、スピーカー駆動力と振動板位置の関係を表にします。
| 信号周波数 |
駆動力と振幅の関係 |
| f0未満の低域 |
常に 駆動力最大=振幅最大 |
| f0以上の周波数 |
過渡応答では 駆動力最大=振幅最大
定常状態では 駆動力最大=加速度最大 |
『駆動力最大=振幅最大』の領域では、『振動板の位置=信号強度』とも言えます。
『駆動力最大=加速度最大』の領域では、振動板の位置が入力信号と位相のずれを起こします。
そういえば、スピーカーによる低域再生で「位相補償が必要」とかいう話題があったような気がします。
定量的評価をしたい人へ
ここまで定性的な説明ばかりしてきました。
実際に定量的評価をしたい人は、運動方程式を立ててください。
小音量時の低音再生と駆動方式に書いた摩擦の話まで考慮すると、面倒になります。
- F = kx + ma + μ (k はバネ定数、xは振幅、mは振動板の質量、aはxの時間2階微分、μは摩擦力)
- F = Y sin(ωt) (電流駆動を想定し Yは振幅、ωは振動周波数の2π倍)
定常状態ではxは振動周波数ωのsin波になり、入力信号と振動板運動の位相差は周波数で変化するはずです。
方程式を軽くいじってみる
先の連立方程式を変形します。
kx + ma + μ = Y sin(ωt)
x を単純な振動と仮定し、x = A sin(ωt + θF)とおきます。
A(k - m ω2) sin(ωt + θF) + μ = Y sin(ωt)
便宜上μ = 0とします
A(k - m ω2) sin(ωt + θF) = Y sin(ωt)
- k > m ω2 のケース
θF = 0、A = Y / (k - m ω2)
- k < m ω2 のケース
θF = π、A = Y / (m ω2 - k)
- k = m ω2 のケース
左辺が0になって計算不可能(μ=0とおかなければ有限値)
x = A sin(ωt + θF) とおかなければ、別の解が出てくる可能性もあります。
真面目に微分方程式を解くことができれば、f0よりも高い周波数で過渡応答から定常状態へ位相が変化してゆくのも観察できると思います。
電圧駆動で考えてみる
連立方程式の2番めの式は、電流駆動でした。
こちらから電圧駆動の F = Y sin(ωt - θ) / √(R2 + L2 ω2) を持ってくるとこうなります。
- k > m ω2 のケース
θF = -θ、A = Y / (k - m ω2) / √(R2 + L2 ω2)
- k < m ω2 のケース
θF = π - θ、A = Y / (m ω2 - k) / √(R2 + L2 ω2)
- k = m ω2 のケース
左辺が0になって計算不可能(μ=0とおかなければ有限値)
力学的エネルギーの供給から制動を考える
振動板の運動が求まったので、運動のために必要なエネルギーを計算し、エレクトロニクス上で余分に必要となる電圧もしくは電流を求めます。
電流駆動の場合
振動は、周期的に必要なエネルギーが変動するので、時間あたりの消費エネルギーの瞬間値を求めます。
WF = F v {vはxの時間1階微分}
v = A ω cos(ωt + θF) と F = kx + ma、x = A sin(ωt + θF) を代入
WF = A2 ω (k - m ω2) sin(ωt + θF) cos(ωt + θF)
電流駆動では電流I = X sin(ωt) が決まっていて、力学的エネルギー補給のために電圧Vが変化します。
先に求めておいた θF = π、A = Y / (m ω2 - k)も代入すると
⊿V = WF / I = (Y2/ X) (ω / (m ω2 - k)) cos(ωt)
電圧駆動の場合
電流駆動と同様に WF = F v に以下を代入します。
v = A ω cos(ωt + θF) 、 x = A sin(ωt + θF) 、θF = π - θ、A = Y / (m ω2 - k) / √(R2 + L2 ω2)、V = X sin(ωt)
すると⊿I = WF / V = (Y2/ X)(1 / (R2 + L2 ω2)) (ω / (m ω2 - k)) sin(ωt - θ)cos(ωt - θ) / sin(ωt)
制動の根拠
電流駆動の⊿Vも電圧駆動の⊿Iも分母に m ω2 - kが出てきます。つまり、振動角速度ω = √(k/m)の共振状態になると、⊿V、⊿Iが±無限大に発散します。
アンプの出力電圧、出力電流を±無限大まで増やせないことが、制動の根拠です。
電流駆動でも制動は効きますね。
電圧駆動の⊿Iは、sin(ωt)=0の前後でも±無限大に発散します。
電圧駆動では、余分なタイミングでも制動がかかっているわけですね。
出力電圧、出力電流に余裕のあるアンプほど制動が効きにくくなります。
ダンピングファクターはここにも影響するのかも知れません。
あまり出力に余裕のあるアンプを接続してしまうと、電力供給限界の前にスピーカーユニットの底づきが発生します。
スピーカーのインピーダンスグラフに出てくる共振時のピークインピーダンスの話は、こちらに書きました。
微分方程式をまじめに解いてみる
Mathematicaで微分方程式を解いてみます。
ma + μv + kx = A sin(ωt)
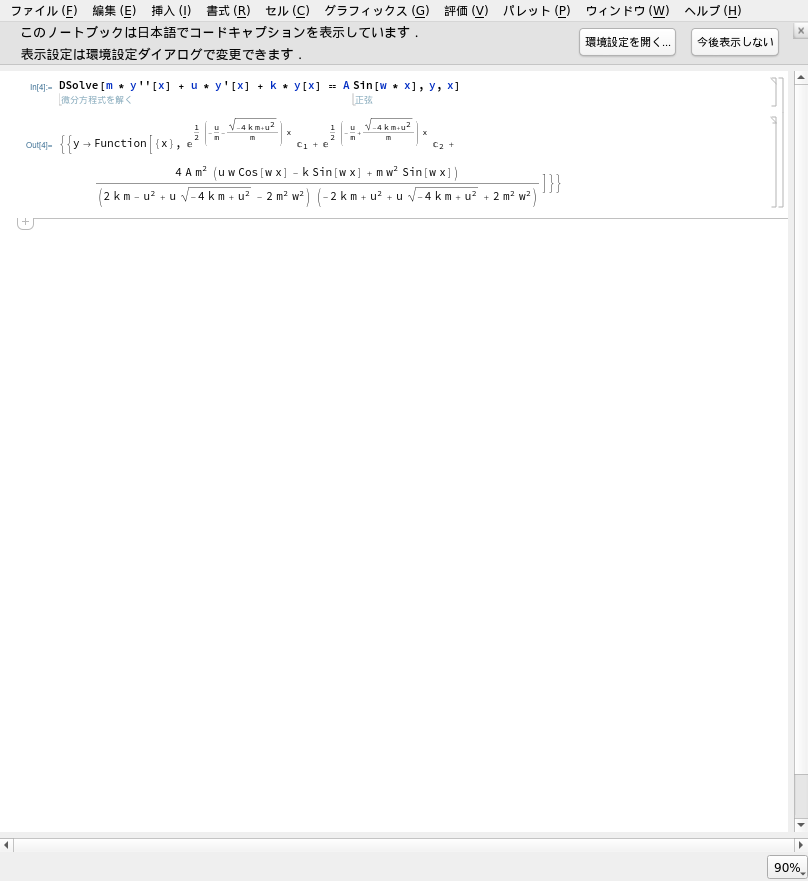 図3 mathematicaで微分方程式を解いたところ
図3 mathematicaで微分方程式を解いたところ
摩擦力は、運動の方向によって向きが変わるので、運動速度に比例するものとして近似しています。
他にも近似はいろいろあります。
摩擦力は、速度が0になると静止摩擦、運動中は動摩擦になりますし、摩擦力がコーンにかかる力の合計を超えることはありませんが、運動速度に比例した定数にしました。
細かいことを言い出せば、ばね定数kも電磁気的駆動力係数Aもx(t)の値によって変化しそうですし、厳密な話は数値シミュレーションするしかなさそうです。
 図4 式を整理する
図4 式を整理する
c1と c2が係数になっている項は、初期状態の影響を示します。
exp()の引数が負の数と虚数の和になっているので、減衰振動です。
最後の項が磁力による駆動の振動を示します。
振幅を示す定数係数に、駆動力の係数、スピーカーコーンの質量、サスペンションのばね定数、摩擦力、角速度(周波数に比例)が出てきます。
振動関数はsin(ωt)とcos(ωt)の定数倍の和です。
cos()の項は、摩擦力による振動の遅れを示しています。
f0の影響を考える
図4の最後の式に、f0条件(ω=√(k/m))を代入してみてください。
sin()の係数が0になりcos()の係数が残ります。
また定数係数部分は、分数の分母が0にはなりません。
よって振動は無限大に発散したりしません。



