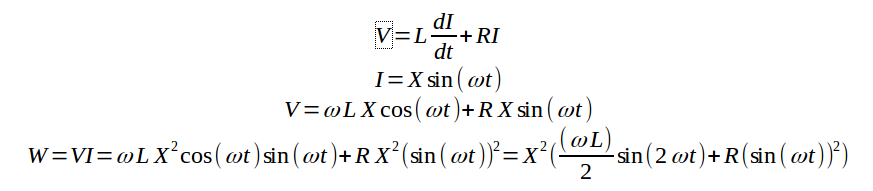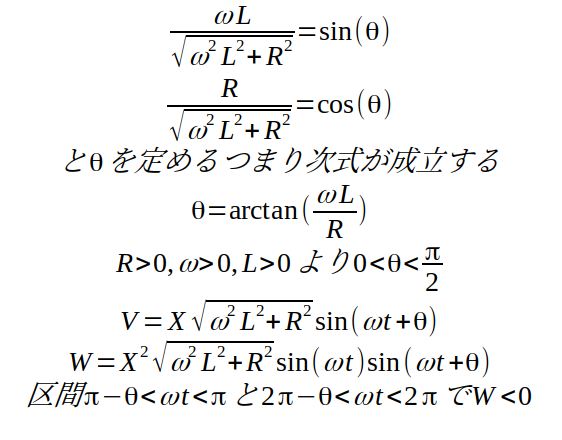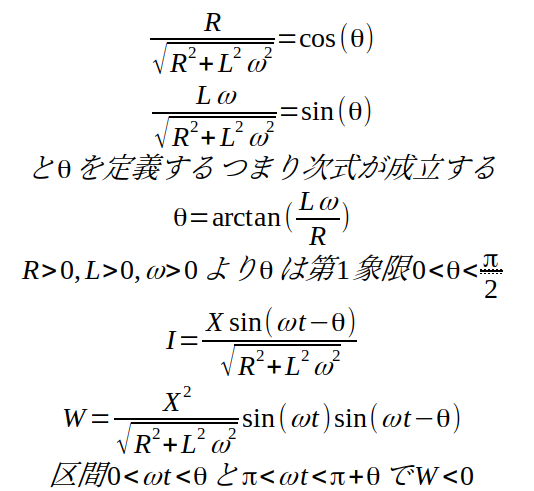スピーカーの電流駆動理論
現在位置のナビ
トップ → コンピュータの国 → 雑記帳 → 趣味趣味音響 → スピーカーの電流駆動理論
説明
なぜ電流帰還アンプにこだわるのか?
でも書いたように、Webmasterはスピーカー駆動を電流基準で考えるべきだと主張します。
主張の根拠は、均一な磁界の中で電磁石が発する力は、電磁石に流れる電流に比例するからです。
オーディオ界ではいまだに電圧で考えるのが常識のようですが、この考え方は物理学の常識に反しています。
どうしても電圧基準で考えたいのであれば、Maxwellの方程式を置き換える目的で現行の物理学とも電圧基準のオーディオとも矛盾しない理論を確立してください。
「♪できるもんならやってみな!はいっ(爆風スランプ談)」
ここでは、電流基準でスピーカー駆動を考えながら、数式をいじって過去のオーディオ界で観測されたあれこれを説明してみます。
理解のためには、大学の理工学部相当の知識と能力が必要です。
エレクトロニクスの回路部品モデルとしての電磁石
まず数式で扱うために、スピーカーの電磁石を回路部品モデルにします。
スピーカーから空気振動として出ていくエネルギーを考えなくて済むように、電磁石が接着剤で固定されていて音は出ないものと考えます。
空気振動まで考えるのは今日はやめといて、電流駆動のあれこれを解決した後にします。
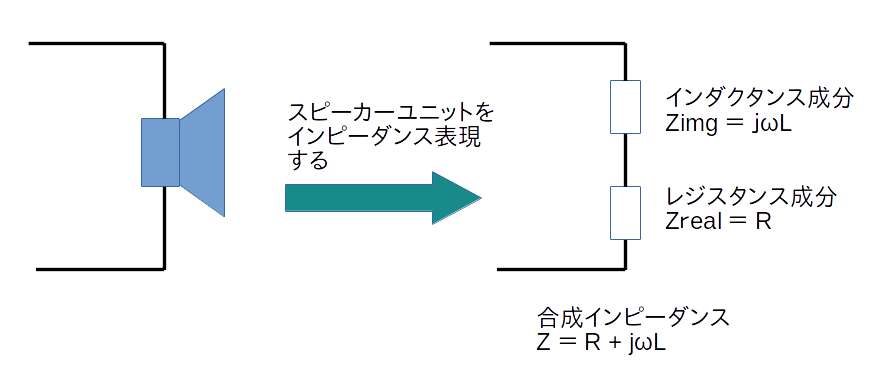 図1 スピーカーユニットをインピーダンス表現する
図1 スピーカーユニットをインピーダンス表現する
スピーカーユニットの電磁石をモデル化したのが図1です。
電磁石のコイルはインダクタンス成分Lとなります。
コイルの導線は抵抗成分を持ちます。
スピーカーユニットの両端にテスターをつないでDC抵抗を測るとゼロにはなりません。
この値をRとします。
Fostex社のWEBサイトからFE103Enのインピーダンスを読み取る
数式に具体的な数値を当てはめる必要があるので、実際のユニットの値を取得します。
幸い、Fostex社のサイトにFE103Enの合成インピーダンスのグラフがあるので、ここから有効数字1桁程度の数値を読み取ります。
メカニカルな共振周波数付近を除外すれば、低域のインピーダンスは8Ωです。
R=8[Ω]としてよいでしょう。
20kHzで合成インピーダンスの絶対値が32Ωです。
ωL=√(32 x 32 - 8 x 8) ≒ 30[Ω]
なのでL=30/ω=30 / (2 x π x 20000)≒240[μH]
としましょう。
電流駆動の電圧、電力を求める
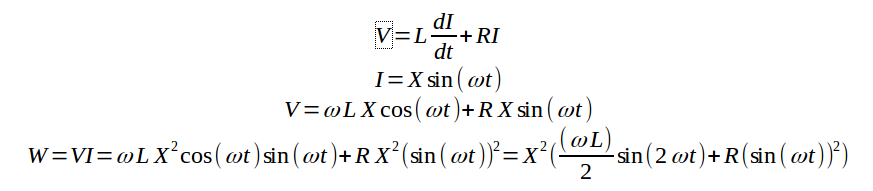 図2 電流駆動の電圧と電力
図2 電流駆動の電圧と電力
数式の簡単な電流駆動から説明します。
電流I=X sin(ωt)
でスピーカー駆動するときの電圧、電力を図2に示しました。
Xは振幅です。
供給電圧、供給電力は、振幅が同じならば周波数に比例して大きくなる
電圧Vを示す式には項が2つあります。
前者がインダクタンスで発生する電圧で、後者が抵抗成分で発生する電圧です。
インダクタンスで発生する電圧は、周波数に比例しています。
前者はωに比例しているので、周波数に比例して大きくなります。
FE103Enのデータ(R=8、L=240μ)とX=1/8を代入して電圧の最大値を求めると、抵抗成分による電圧降下は常に1[V]ですが、インダクタンス成分による瞬間最大電圧降下は、20Hzで3.75mV、20kHzで3.75Vになります。
電力も、同様にωLに比例する項があるので、周波数が高くなるほど要求電力も大きくなります。
供給電力は、±の値を取る
電力Wを示す式の第1項はsin(2ωt)に比例し、第2項はsin(ωt)の2乗に比例します。
第2項は常に正ですが、第1項は負にもなります。
ωが大きくなると、2つの項の合計値であるWは負の値を取るタイミングがあります。
エネルギーがマイナスということは、スピーカーユニットからアンプに対してエネルギーが戻るタイミングがあるということです。
アンプ側スピーカー駆動回路で、電圧と電流の符号が逆の組み合わせを取ることを想定した回路になっているでしょうか?
インダクタンスへ送ったエネルギーは返ってくる
物理学を真面目に勉強した人には当たり前のことですが、インダクタンスに送った電気エネルギーは磁場の形で蓄えられて、消費されなければ駆動回路に戻ってきます。
一時的には周波数に比例したエネルギーが必要に見えますが、ほとんど消費されずに返ってくるので、長い目で見ると収支はバランスしています。
ただ、一時的に大きなエネルギーが要求されるのに応える回路、戻ってきたエネルギーを再利用する回路が求められます。
電流駆動アンプでは「(供給電圧が)大きいことはいいことだ」が成り立ちますね。
電圧駆動の電流を求める
 図3 電圧駆動の電流
図3 電圧駆動の電流
今度は電圧駆動の話です。
図3に式を示します。
電流→電圧の計算は簡単でしたが、逆方向は面倒くさくなります。
微分方程式を解かなければなりません。
Webmasterは、去年眠れない晩に起き出して、20年ぶりに微分方程式を解きました。
念の為、GNUのRで検算してあります。
電流を示す項は4つになりました。
そのうち第1項、第2項は、初期条件の影響を示す式であり、定常状態では無視できます。
ちなみに、t=0を代入すると、第3項は単独でゼロになり、第1項と第4項が相殺されて第2項だけが残ります。
I=I 0となり、I 0は時刻0での電流値を示すので、当たり前の結果となります。
定常状態を考えるとインピーダンスで計算することもでき、第3項、第4項と一致します。
ωt=0のとき、第3項は0になりますが、第4項は負の値になります。
電圧基準アンプでも、エネルギーが返ってくるタイミングがあります。
ωt=0なので、電圧が0になる瞬間ですけど。
図3の式から、いろいろ考察できます。
いままで、オーディオ界で提唱されてきた工夫の全てとは言わないまでもその多くが、電圧駆動による弊害をその場しのぎの対策で乗り切ったものではないかと、webmasterは考えます。
次節以降で書いてみましょう。
電圧駆動アンプは高域再現が苦手
図3の第3項+第4項が、スピーカーの電磁石が作る磁場の強さと比例します。
ωが大きくなるとどうなるでしょうか?
R 2 << (Lω) 2となるので、分母はほぼω 2に比例します。
すると第4項は1/ωに比例するので、周波数に反比例して電流が減少し、スピーカーの駆動力もそれに比例して減ります。
逆に低域はどうでしょうか?
lim ω→0を考えると、電流駆動も電圧駆動も抵抗成分での電圧降下が支配的になるので、ほぼ一致します。
DC出力するのに電圧駆動も電流駆動もほぼ同じわけですね。
項が2つある影響はどうでしょうか?
第3項はωが十分大きくなると第4項よりも小さくなり無視できます。
第3項と第4項の絶対値がほぼ同じになるのは、FE103Enの数値を用いると5kHzあたりですね。
第3項はsin(ωt)に比例し第4項はcos(ωt)に比例するので、位相が90度ちがいます。
ωの値によって、電流の位相が変わってきていますね。
Webmasterは、電圧駆動アンプで高域再現が悪いことが、ラウドネス特性を決める原因の一つになったと予想しています。
電圧駆動で高域再現が悪いのは出力が大きいときも小さいときも同じなので、一見すると小音量とは関係なさそうに見えます。
これは、「小音量では高域を持ち上げないと耳の最低感度を超えないから」という理屈で説明できます。
大音量でも高域は不足していますが、聴くことはできます。
音量の違いは、「耳の音量感度がリニアではなくてlogスケールだから、気になりにくい」と考えます。
低域についてラウドネスの補正が必要なのは、エレクトロニクスではなくてスピーカーコーンのエッジにおける摩擦に原因があると考えています。
すでにモデル化は終わっているので、いつか説明します。
電圧基準の世界では歪率もf特も測る意味がない
オーディオ界で現行の測定基準では、アンプの歪率もf特も出力電圧を測定しています。
スピーカー出力が電流に比例するのであれば、アンプ出力の電圧を測ることにあまり意味はありません。
ここまでの議論に納得した人であれば、電圧で測定したアンプ特性を電流特性に置き換えることができるかもしれませんが、そんなことをするくらいならば電流を測ったほうが早いでしょう。
電流駆動の電力式を見ると、sin(2ωt)が出てきます。
もしも、電流駆動のアンプ出力を電力基準で測定したら、「2倍高調波が出ている」と勘違いする人が続出することでしょう。
電圧基準ではsinとcosの和になりますが、測定器が純粋電圧を測定しているのか、電力から間接的に電圧を測定しているのか、あなたは即答できますか?
YAMAHAのサイトで電流帰還アンプ製品を調べると、「カタログスペックよりも聴感上の音質を優先させたピュアオーディオ仕様の電流帰還型回路を全チャンネルに採用し、より豊かな音の表現力や伸びやかな空間再現、そして圧倒的な力感をあらゆるソースで実現します。」という記述があります。
もはや電圧基準の歪率、f特を自慢することは、恥ずかしい世界になりそうです。
ダンピングファクターってこういうこと?
オーディオ界には、ダンピングファクターという言葉があります。
Webmasterは、このダンピングファクターを物理学の世界にうまく当てはめることができません。
そもそも、スピーカーインピーダンスとアンプの出力インピーダンスの比をとっているはずなのに、複素数ではなく実数で表現されます。
しかも、同じダンピングファクターの数値の機械を並べても、聴感上の特性はバラバラです。
Luxmanのサイトに書かれたダンピングファクターの説明も意味不明なので引用します。
「ダンピングファクターの値が小さいと、アンプからスピーカーに送り込んだ音楽信号の電流が逆起電圧を発生させ、それによってスピーカーがまた振動してしまうという現象を引き起こしてしまいます。」
アンプからスピーカーに送り込んだ音楽信号の電流が逆起電力を発生させるのは、ダンピングファクターに関係なく常に起きます。
回路素子がエネルギーを受け取るとき、電流をもとに逆起電力が起きるのです。
逆起電力で回路素子からエネルギーが出てくるわけではないので、「それによってスピーカーがまた振動してしまう」という表現はおかしいです。
Webmasterの強引な解釈を、ここに書きます。
みんながダンピングファクターという言葉で表現したかったものは実は、このページで記述した「エネルギーが返ってくる瞬間のアンプ側の応答」ではないでしょうか。
電圧と電流の符号が逆転した状態になったとき、最終段が逆電流を吸い込めないダイオードのような設計となっているアンプからは良い音が聴けなくて、逆電流を柔軟に吸い込める設計だと理想的な電流駆動ができるということかもしれません。
2018年7月17日追記
アンプの出力インピーダンスが高いと、電流が戻ろうとしてもインピーダンスによって電圧が発生してしまい戻りにくくなります。
アンプの出力インピーダンスが低くても、逆電流を吸い込めるかどうかの違いで逆電流の処理が変わってきます。
出力インピーダンスが低くてなおかつ逆電流を吸い込める設計になっている一部のアンプでのみいい音が聞けるという仮説は、ダンピングファクターにまつわる体験談(伝説?)と一致しませんか?
逆電流の問題は、低域でも高域でも発生します。
逆電流が発生している時間は信号周期に比例しますから、低域ほど長く、高域ほど短くなります。
低域ほど逆電流問題を聴き取りやすく、高域ほど力学的なローパスフィルター効果(スピーカー振動部の慣性)で現象がマスクされているのかもしれません。
大音量再生とコンプレッション 2018年7月29日追記
音のディテールを聴き取りたいという目的で、大音量再生する人がいます。
CDのレコーディング・エンジニアは、微小な音を強調するためにコンプレッションをかけたりします。
この2つは、どちらも電圧駆動のフラットではないf特が原因ではないでしょうか。
電流駆動やPDM再生では、電圧駆動と比較して音のディテールが聴き取りやすく、またリアルに聴こえます。
逆に表現するならば、電圧駆動の表現はリアルさに欠けディテールが聴き取りにくいのです。
この電圧駆動の欠点を補うため、ユーザーは大音量再生に走り、レコーディング・エンジニアはコンプレッションかけまくるのではないでしょうか。
嘘だと思うなら、大音量再生に慣れたリスナーや、コンプレッション大好きなレコーディング・エンジニアに電流駆動の音を聴かせてみてください。
認識をあらためてもらえると期待しています。
マルチウェイスピーカー 2018年10月20日追記
突然ですが、「数十年前のオーディオ開発現場はこうだったんじゃないか劇場」をお送りします。
参考にしたのは、webmasterの脳内妄想です。
「スピーカーのインピーダンスって複素数だけど面倒だから抵抗成分扱いして実数で考えちゃえ」
「電圧帰還回路って比較的簡単に実装できるから、オーディオアンプにも適用しちゃえ。スピーカーを抵抗扱いしているから、電流も電圧に比例すると考えていいよね」
「スピーカーに一定周波数のsin波を送ると、V-Iの実効値比率は高域ほど抵抗が大きくなるね」
「高域で音圧が落ちるのは スピーカーの抵抗が大きくなるせいだから、高域になるほど能率が高くなるスピーカーユニットがほしいね」
「高域になるほど能率が高くなるスピーカーユニットをフルレンジのメカ特性でチューニングするのは至難の技だから、ユニットを複数搭載したマルチウェイを作っちゃえ。音域ごとに能率を変えればいいのさ」
「マルチウェイはユニット毎に再生周波数の担当帯域が違う。 電圧基準で信号周波数を分割するネットワークを設計したよ」
「電圧基準で信号周波数を分割するネットワークは、設計通りに働かないから再生音をききながら回路定数を追い込んでいく必要があるね」
「電圧基準でマルチウェイスピーカーを設計する方法論がようやく確立したぞ。D級アンプとか電流駆動のアンプはまだ発明されていない時代の設計だから、電圧帰還アンプ以外つないでもいい音出ないよ」
考え方が間違っているところを、強調表現してみました。
数式の整理 2019年5月17日追記
図2と図3の式を、三角関数の積和の公式を使って整理します。
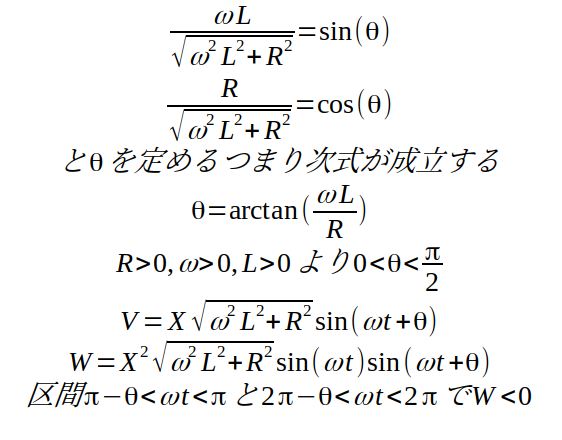 図4 電流駆動の式を整理
図4 電流駆動の式を整理
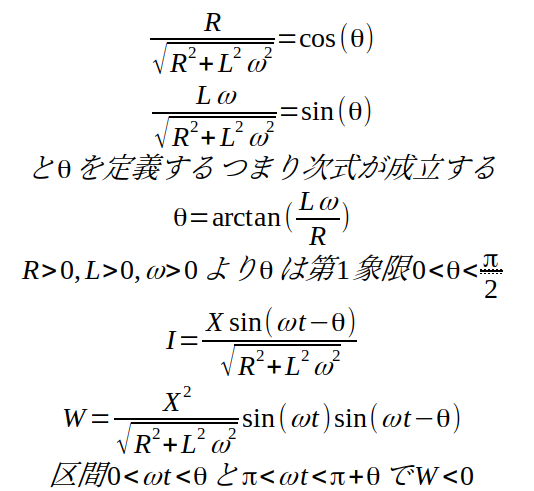 図5 電圧駆動の定常状態式を整理
図5 電圧駆動の定常状態式を整理
2種類のアプローチで計算した式が、同じことを表現するようになりました。
- 電圧の実効値は電流の実効値の√(ω2 L2 + R2)倍になります。
- 電圧は、電流よりもarctan(ωL/R)だけ位相が進みます。
インピーダンス計算に慣れている人にとっては、当たり前のことを言っています。
掲載日
2018年7月14日 初出
2019年5月17日 追記