説明
ここでは PCM(Pulse Code Modulation) の限界について解説をします。
PCM について常識として言い伝えられていることや、
一般的リスナーが予想もしていないような挙動について書きます。
プログラム
| 動作環境 | ファイル | サイズ | バージョン | 日付 |
|---|
| unix & gtk+ |
viewer.tgz 波形表示プログラム |
3,626 Byte |
0.1 | 2004年7月13日 |
| C 言語 |
filters.tgz 波形操作プログラム集 |
2,929 Byte |
0.1 | 2004年7月13日 |
viewer は、ここで紹介するサンプルプログラムの出力を、ウィンドウ画面上で波形として表示します。
オシロスコープのシミュレータと考えてもらってもかまいません。
filters には、波形データを操作するプログラムが入っています。
それぞれのプログラムは、実際に使いながら解説してゆきます。
将来ディジタルオーディオの解説が増えてゆくと、filters の中身も増えてゆくことになります。
PCM で表現できない高い周波数
PCM では、サンプリング周波数の 1/2 までの周波数しか表現できないと言われています。
この点を実際に検証してみましょう。
% wave_gen -Hz 50000 >data2-1
% viewer data2-1
 図2-1
図2-1
図1-5 は周波数 50kHz の波形です。
これをサンプリング周波数 44.1kHz の PCM にしてみましょう。
% pcm <data2-1 >data2-2
% viewer data2-2
 図2-2
図2-2
これがサンプリング周波数の 1/2 より高い周波数を入れたPCM の出力です。
PCM によって、オリジナルとは全く異なる周波数の信号に変換されてしまっていますね。
これをそのまま再生してしまえば、本来存在しなかった信号(すなわちノイズ)の乗った信号となります。
このノイズを避けるためには、PCM の A/D 直前に LPF を入れる必要があります。
サンプリング周波数の1/2 にまつわる神話
情報工学の教科書を読むと、「PCM ではサンプリング周波数の1/2の周波数成分まで伝達できる」と書いてあります。
この記述に間違いはありませんが、サンプリング周波数の1/2の周波数の波形をそのまま伝達できると思ったら大間違いです。
実際に見て行きましょう。
% wave_gen -Hz 22050 >data2-3
% viewer data2-3
 図2-3
図2-3
これを PCM にします。
% pcm <data2-3 >data2-4
% viewer data2-4
 図2-4
図2-4
ちょうど波形が振幅0になる位置でサンプリングしているため、出力が0になってしまいました。
おなじ周波数でも位相をπ/2ずらすと出力が出てきます。
% wave_gen -Hz 22050 -phase 90 | pcm >data2-5
% viewer data2-5
 図2-5
図2-5
位相をπ/4ずらすとこうなります。
% wave_gen -Hz 22050 -phase 45 | pcm >data2-6
% viewer data2-6
 図2-6
図2-6
このように、サンプリング周波数の1/2の周波数を入れても、位相や振幅は保存されません。
教科書に書いてあった意味を解釈すると、「サンプリング周波数の1/2以下の周波数では、その周波数成分が保存されるが位相や振幅は知ったことではない」ということになります。
高域での挙動
サンプリング周波数の1/2までいかなくても、高域になると波形は乱れて来ます。
周波数 20kHz を見てみましょう。
% wave_gen -Hz 20000 | pcm >data2-7
% viewer data2-7
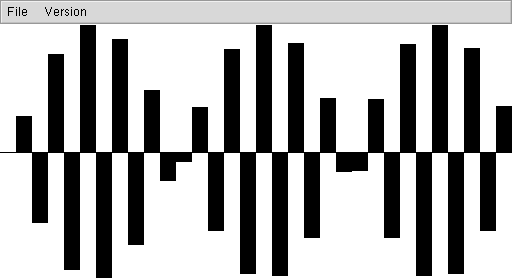 図2-7
図2-7
振幅が大きくなったり小さくなったりしていますね。
このように PCM ではサンプリング周波数の1/2以下の周波数でも高域においていろいろと信号が変化します。
しかし、現実問題としてあまり気にする必要はありません。
先の LPF の部分で書いたように、LPF はある周波数まで100%通しておいてその先をスパッとカットするような特性にはできないのです。
実際には可聴周波数域の上の方から少しずつ減衰してゆきます。
20kHz 〜 22.05kHz の周波数は原理的には伝達できるはずでも、実際問題としてはほとんど伝達できていないのです。






