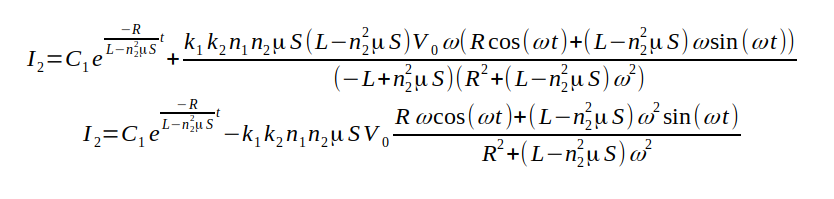現在位置のナビ
トップ → コンピュータの国 → 雑記帳 → 趣味趣味音響 → 真空管アンプの駆動電流
説明
真空管アンプの駆動電流を物理学の方程式を立てて確認しました。
モデル化
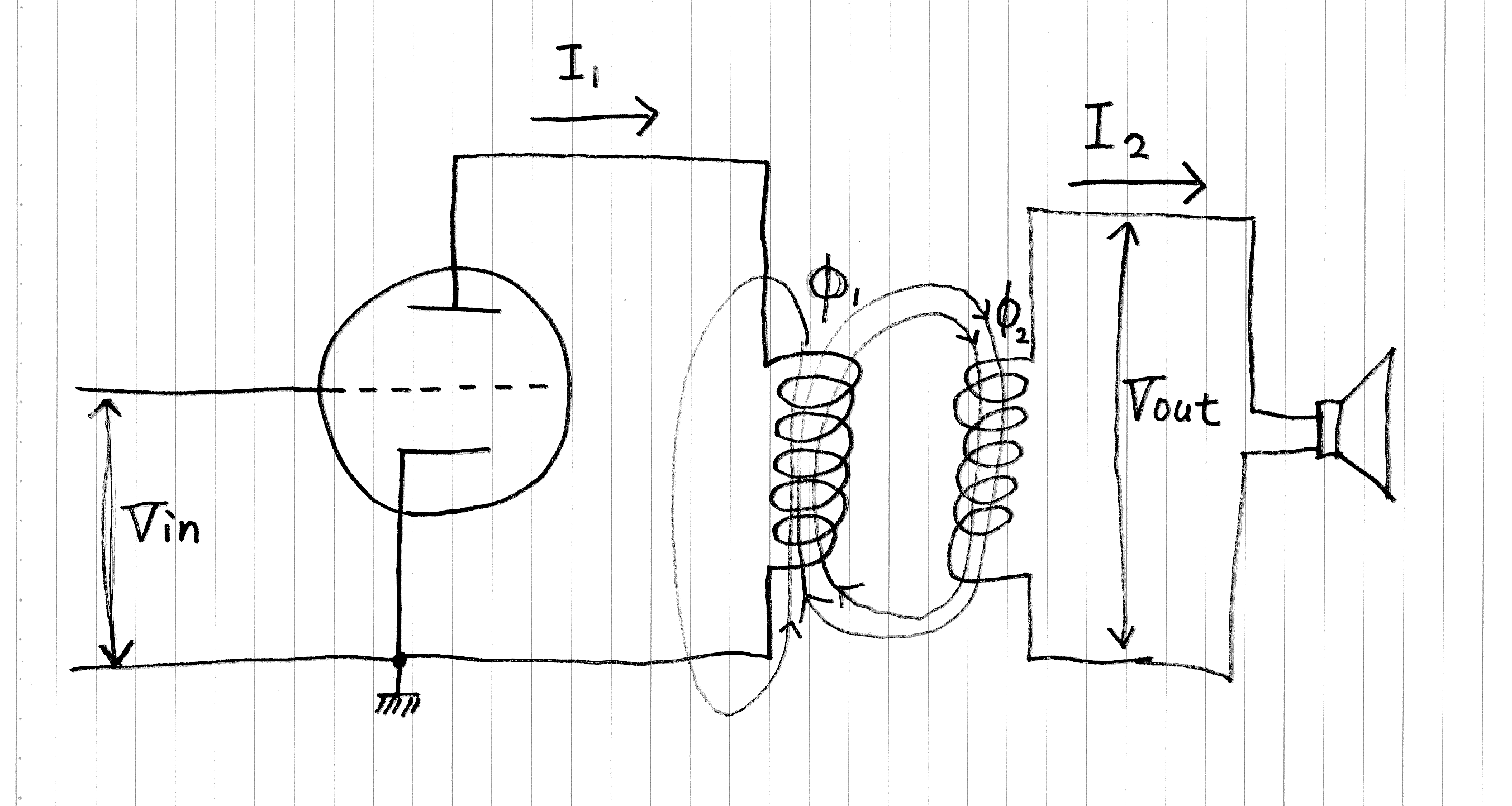 真空管アンプのモデル
真空管アンプのモデル
真空管アンプの増幅部分を単純にモデル化しました。
真空管のアノードって電子が外に出てくるところですから、電流を+からー方向へ書くと I1の矢印は逆向きですね。
- Vin: 入力電圧(Vin = V0 x sin(ωt))
- I1: 真空管からの出力電流
- Φ1: トランス1次側の磁束
- Φ2: トランス2次側の磁束
- n1: トランス1次側の巻数
- n2: トランス2次側の巻数
- μ: トランス鉄芯の透磁率
- S: トランス鉄芯の断面積
- I2: トランス2次側の出力電流
- Vout: トランス2次側の出力電圧
真空管の出力電圧は、出力電流と負荷回路から決まるものとします。
アノードに到着する電子が持つエネルギーと、真空管出力の電流、電圧とのエネルギー差は、アノードの発熱で吸収するものとします。
I1 = Ic + k1 x Vin
{Icは電流オフセットk1は比例定数}とします。
I1 = Ic + k1 x (V0 x sin(ωt))…式(1)
トランスの1次、2次の間でロスを引いた磁束の割合を {k2: 1 ≧ k2 ≧ 0}とすると、
Φ2 = k2 Φ1 - μ n2 I2 S…式(2)
トランスの1次側の磁束と電流の関係 Φ1= μ n1 I1 S …式(3)
トランスの2次側の磁束と電圧の関係 Vout= - n2 (d Φ2/ dt) …式(4)
トランスの2次側の電流は電圧とスピーカーインピーダンスより決まる Vout= R I2 + L (d I2/ dt) {スピーカーインピーダンスは R+jωL} …式(5)
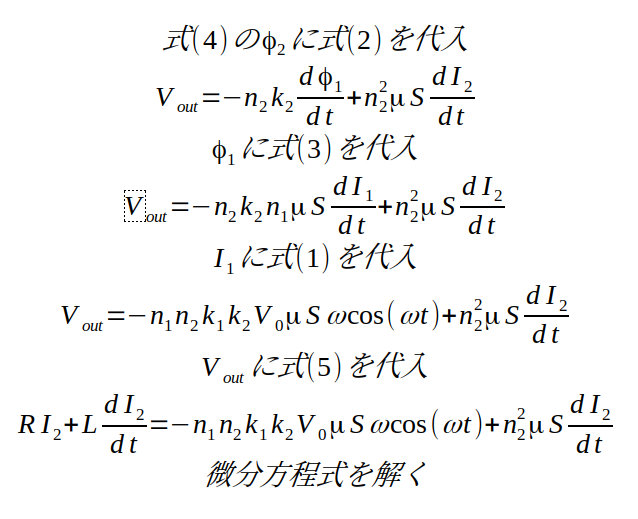 方程式を解く(前半)
方程式を解く(前半)
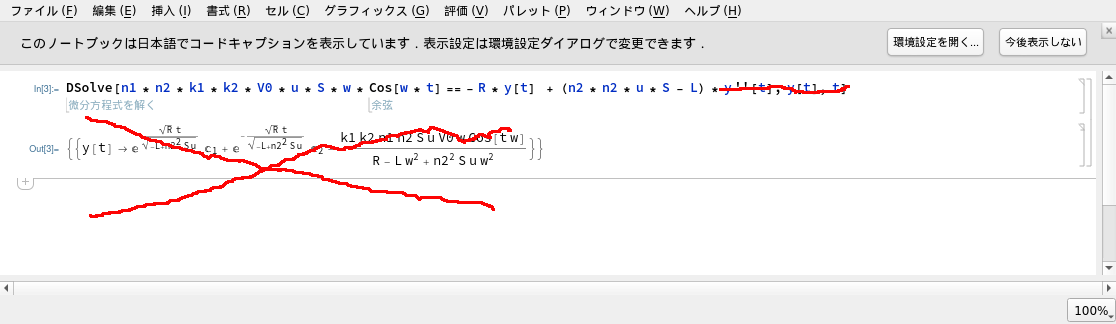 間違った微分方程式
間違った微分方程式
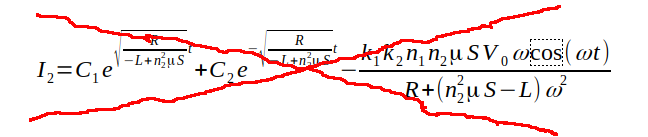 間違った解
間違った解
微分方程式を解くところから仕切り直し
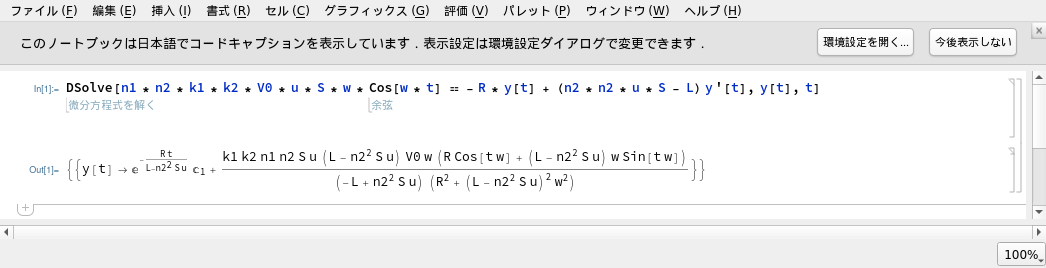 mathematidaで微分方程式を解く
mathematidaで微分方程式を解く
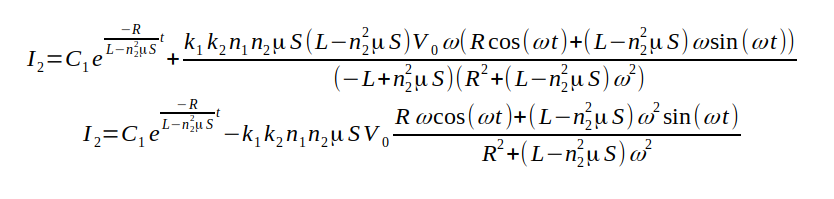 微分方程式の解
微分方程式の解
間違った解の評価
うーむ。
予想外の式が出てきました。
計算結果合っているのかな?
I2を示す第1項と第2項で、exponentialの指数が逆転しています。
片方が単調減少だったら、もう片方は単調増加になります。
それとも平方根の中が負になって振動するのでしょうか?
I2を示す第3項が、スピーカーを駆動する主な電流のはずです。
真空管の入力電圧はsin(ωt)に比例していたのに、出力電流は-cos(ωt)に比例するので位相が90度変わります。
第3項の分数のうち分子はωに比例して、分母にはω2の項があるので、周波数が高くなるほど出力は小さくなります。
電圧駆動に近いですね。
I2を示す第3項には、スピーカーインピーダンスのRとかLの他に、トランスの特性であるμとかSとかn1 n2が出てきます。
トランスを入れ替えると出力特性が変わるわけですね。
評価
複雑な式になりましたが、今度は合っていそうです。
初期状態が影響する C1の項は、時間に連れて減少します。
第2項がスピーカーを駆動する電流です。
ωが小さいとき(低周波)では、分数が(ω/R)cos(ωt)に近くなります。
ωが大きいとき(高周波)では、分数がsin(ωt)に近くなります。
低周波は出にくそうですね。
DCを伝えられないトランスの特性が出てしまっています。
また低周波では位相が90度近く進みます。
電圧駆動と違って、高周波でも出力は小さくなりません。
フルレンジスピーカーを鳴らしても、高域がちゃんと出てきます。
なるほど、「真空管アンプが電圧駆動のトランジスタアンプよりいい音だ」という人がいるわけです。
Webmasterとしては、高域が理想的出力なのに、低域になるに従って位相も振幅も変動するのが気になります。